Info IV, Tutorium 2, SS07

Dies ist die Homepage zum Informatik IV Tutorium Nummer 2 im Sommersemester 2007 an der Universität Karlsruhe (TH).

Ort: Raum -109 im Informatik Neubau (Geb. 50.34)
Zeit: Wöchentlich – Montag, 11:30 Uhr; erstmalig am 23. April 2007
Kontakt: thomas.pajor (at) logn.de oder #uka.info1 im Quakenet

Einen Übungsschein könnt ihr erwerben. Hierfür sind mindestens 2/3 der zu erreichenden Punkte auf den Übungsblättern nötig.

Die Abgabe in Zweiergruppen ist nicht erlaubt. Dafür wird es immer nur eine Korrekturaufgabe á 10 Punkte pro Übungsblatt geben.

Die bearbeiteten Übungsblätter sind, wie gewohnt, versehen mit Name, Matrikelnummer sowie der Tutoriumsnummer in die Einwurfsschlitze im Keller des Informatik Neubaus zu werfen. Bitte achtet darauf dass eure Blätter zusamengetackert sind.

Begleitend zur Vorlesung gibt es außerdem eine Newsgroup in der diskutiert und Fragen gestellt werden können.

Neues…

Ende

Samstag, 28.07.2007, 15:36

Das war es dann mit den Tutorien dieses Semester. Unsere (korrigierten) Folien sowie die Lösung zur Simplex-Aufgabe aus dem Zusatztutorium habe ich unter Material verlinkt. Ich hoffe es hat euch trotz des nicht ganz einfachen Stoffes Spaß gemacht. Bleibt mir schließlich nurnoch viel Erfolg für die Klausur zu wünschen, und falls ihr noch Fragen habt könnt ihr mich natürlich weiter via Elektropost erreichen (Wobei ich jedoch bis mitte August nicht in Karlsruhe sein werde).

Vielen Dank wieder an Adam Taras für die regelmäßigen Aufzeichnungen und an alle die Hinweise zu Fehlern auf Folien oder den Lösungen gegeben haben. :-)

Zusatztutorium

Mittwoch, 18.07.2007, 23:14

Ich habe es ja schon im letzten Tutorium angekündigt: Ein Zusatztutorium gehalten von Benjamin Vogel (Tut 7) und mir zur Klausurvorbereitung wird es geben! Termin und Ort stehen jetzt fest und sind:

Freitag, 27. Juli, 14:00 Uhr – Hörsaal -101 Infobau (Geb. 50.34)

Wir werden allerdings keinen eigenen Stoff vorbeiten. Bitte stellt Fragen und Themenwünsche vorher via Elektropost, so dass wir dazu was vorbereiten können. Ihr seid natürlich alle eingeladen teilzunehmen, egal ob ihr in unseren Tutorien eingeschrieben seid oder nicht.

Punktestand

Mittwoch, 18.07.2007, 21:10

Ich habe das 11. Übungsblatt korrigiert und die Punkte eingetraten. Außerdem findet ihr schon das 12. Übungsblatt in dem System – allerdings noch ohne Punkte, da ich es ja noch nicht korrigiert habe.

Ergänzungen zum Tut (Wavelet-Transformation)

Dienstag, 17.07.2007, 01:24

Da ich leider nicht alles, was ich zu Wavelets vorhatte, geschafft habe, hier die versprochenen Ergänzungen. Nochmal zur Erinnerung. Der Vektorraum $V_j$ enthält alle abschnittsweise konstanten Funktionen auf dem Intervall $[0,1)$ auf $2^j$ gleich großen Abschnitten, und es gilt

V_j \subseteq V_{j+1}

Die Haar-Basis von $V_j$ sind gerade die Funktionen, die in genau einem Abschnitt den Wert $1$ annehmen und sonst $0$ sind. Davon gibt es natürlich $2^j$ Stück, und alle Funktionen (Bilder) aus $V_j$ lassen sich durch Linearkombinationen dieser Basisvektoren darstellen.

Nun hatten wir noch das Standardskalarprodukt auf Funktionenräumen definiert:

\langle f,g\rangle := \int_0^1 f(x)g(x) \; dx

und somit können wir den Begriff der Orthogonalität verwenden (Zur Erinnerung: Zwei Funktionen sind genau dann orthogonal, wenn ihr Skalarprodukt $0$ ergibt). Wegen $V_j \subseteq V_{j+1}$ ist $V_j$ ein Untervektorraum von $V_{j+1}$ und somit existiert bezüglich $\langle \cdot, \cdot \rangle$ ein orthogonaler Komplementraum zu $V_j$ , den wir mal $W_j$ nennen wollen. Weil alle diese Räume endlichdimensional sind, gilt sogar

V_j \oplus W_j = V_{j+1}

Die Basisvektoren von $W_j$ heißen Wavelets. Im Falle der Haar-Basis von $V_j$ betrachten wir die korrespondierte Basis im Orthogonalraum, und definieren

\Psi_j^i(x) := \Psi(2^jx -i) \qquad i \leftarrow 0, \ldots, 2^j-1

mit

\Psi(x) := \left\{\begin{array}{rcc}1 & \text{für} & 0 \leq x < \frac12 \\ -1 & \text{für} & \frac12 \leq x < 1 \\ 0 & \text{sonst} & \end{array}\right.

als Haar-Wavelets. Die folgende Grafik zeigt die Haar-Wavelets für den Raum $W_2$ .

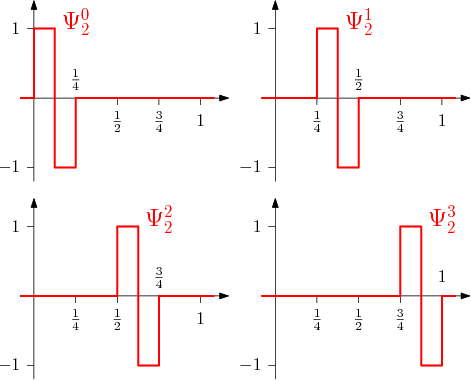
Haar-Wavelets

Man kann relativ leicht einsehen, dass hier je zwei Basisvektoren aus $V_j$ und $W_j$ orthogonal sind, und somit ist $V_j \oplus W_j = V_{j+1}$ erfüllt (Das ist in der LA-Vorlesung vermutlich bewiesen worden). Wir haben in dem einführenden Beispiel auf den Folien gesehen, dass das Eingabebild bei der Wavelet-Transformation sukzessive „vergröbert“ wird, und wir uns jeweils die „Detailkoeffizienten“ dazuspeichern. Die Zerlegung von einem Bild aus $V_{j+1}$ in Komponenten aus $V_j$ und $W_j$ entspricht genau dieser Vergröberung, denn das Bild aus $V_j$ enthält nurnoch halb so viele „Bildpunkte“ (Abschnitte auf $[0,1)$ ) wie das Bild aus $V_{j+1}$ . Der Anteil aus $W_j$ , der für die Beschreibung von dem Bild aus $V_{j+1}$ notwendig ist, lässt sich anschaulich mit den „Detailkoeffizienten“ aus dem Beispiel identifizieren.

Ist nun $f$ ein beliebiges Bild aus $V_n$ , so ist $f$ eine Linearkombination aus Vektoren der Haar-Basis zu $V_n$ .

f = \sum_i c_n^i \Phi_n^i

Dabei sind die Koeffizienten $c_n^i$ genau die Farbwerte der Pixel. Wenn man nun diesen Zerlegungsschritt $n$ mal durchführt so ergibt das gerade

\begin{align*} f &= \sum_i c_n^i \Phi_n^i \\ &= \sum_i c_{n-1}^i \Phi_{n-1}^i + \sum_i d_{n-1}^i \Psi_{n-1}^i \\ &= \dots \\ &= c_0 \Phi + \sum_i d_1^i \Psi_1^i + \dots + \sum_i d_{n-1}^i \Psi_{n-1}^i \end{align*}

Die Wavelet-Transformierte des Bildes ist dann

[ c_0, d_1^0, d_1^1, \ldots \ldots,d_{n-1}^0, \ldots, d_{n-1}^{n-1} ]

Auf den Tut-Folien (siehe Material) ist auch nochmal das Beispiel, das wir eingangs zur Motivation der Wavelet-Transformation durchgegangen sind, auf diese formale Methode bezogen. Außerdem habe ich ein Paper verlinkt, nach dem sich auch meine Herleitung im Tutorium gerichtet hat. Ich empfehle es euch auf jeden Fall als Ergänzung zu dem offiziellen Manuskript.

Korrekturaufgabe auf Blatt 9

Dienstag, 25.06.2007, 13:02

Auf einer frühen Fassung des 9. Übungsblattes sind zwei Aufgaben als Korrekturaufgaben markiert. Dies ist ein Fehler, und es wird nur die Aufgabe 33 korrigiert.

Auf der aktuellen Version des Blattes im Netz müsste das schon berichtigt sein.

Ergänzungen zum Tut heute

Dienstag, 29.05.2007, 19:49

Ich habe heute eine sigmoide Funktion im Tut als monoton (steigend) und mit negativem wie positivem Grenzwert definiert. Dies reicht aber nicht aus! Die Funktion muss weiterhin auch differenzierbar auf dem ganzen Definitionsbereich sein. Damit fällt die Sprungfunktion $h(p)$ mit

h(p) := \left\{\begin{array}{ccc}1 & \text{für} & p \geq 0 \\ 0 & \text{sonst} & \end{array}\right.

weg, da sie an der Stelle $p = 0$ nicht diff’bar ist.

Der Backpropagation-Algorithmus würde nämlich sonst nicht mit beliebigen sigmoiden Funktionen funktionieren, da wir ja die erste Ableitung von $h$ benötigen.

Des Weiteren scheint es in der Literatur mit den Begriffen „Erregungsfunktion“ und „Aktivierungsfunktion“ ein bisschen durcheinander umherzugehen. Ich habe im Tut heute die gewichtete Summe als Erregungsfunktion bezeichnet, also beispielsweise

p_j = \sum_i w_{ij}q_i - \sigma_j

und die Aktivierungsfunktion ist dann beispielsweise die sigmoide Funktion $h(p)$ die den Zustand des Neurons berechnet und $p_j$ als Eingabe bekommt. Im Goos 4 wird mit den Begriffen anders gehandhabt – nur damit ihr nicht verwirrt seid falls ihr in der Literatur rumstöbert.

Verlegung des Tuts am 28. Mai 2007 / Übungsblätter

Mittwoch, 23.05.2007, 14:47

Da nächsten Montag Feiertag ist (Pfingstmontag) werde ich das Tutorium in dieser Woche verschieben. Der neue Termin ist

Dienstag, 29. Mai um 15:45 Uhr in Raum 301 im Infobau.

Danach findet es natürlich wieder zu den gewohnten Zeiten am üblichen Ort statt. Aufgrund der Hochgradigkeit des aktuellen Themas braucht ihr das Übungsblatt 5 erst am Freitag einzuwerfen, und für das nächste Übungsblatt habt ihr dann zwei Wochen Bearbeitungszeit.

Zusatzmaterial; „Themen“-Sektion entfernt

Montag, 21.05.2007, 23:56

Unter „Material“ findet ihr das Java-Applet zur Perzeptron-Lernregel von heute, falls ihr damit selbst nochmal rumspielen wollt. Es war ja etwas hektisch heute am Ende im Tutorium. Außerdem habe ich noch eine Zusammenfassung von Benjamin Vogel (Tut 7) zum (algebraischen) Simplex-Verfahren verlinkt.

Des Weiteren habe ich mal die „Themen“ und die „Material“ Seiten vereinigt. Erstens muss ich dadurch weniger updaten, und zweitens ist es so übersichtlicher, wenn ihr bei den Folien bzw. Aufgaben gleich seht was das Thema im Tutorium war. :)

LP Solve

Dienstag, 08.05.2007, 14:33

Falls ihr ein bisschen mit linearen Programmen rumspielen wollt, so könnt ihr euch mal LP Solve anschauen. Damit könnt ihr ziemlich einfach (ganzzahlige) lineare Programme lösen. Ich habe das außerdem mal unter Material mit verlinkt!

Zum algebraischen Simplex-Algorithmus

Montag, 07.05.2007, 21:56

Ich habe leider heute nicht alles geschafft, was ich machen wollte, und ich weiß nicht ob auf dem nächsten Übungsblatt nochmal was zu Simplex drankommt, und eigentlich will ich mich jetzt auch nicht ewig mit dem Thema aufhalten, deswegen hier noch das, was es zum algebraischen Simplex zu sagen gibt.

Nur nochmal zur Erinnerung. Die Normalform unseres linearen Programms ist ja zu Anfang gerade:

z = c^\top x + v \quad \text{unter} \quad y = Bx + b

wobei $y \in \mathbb{R}^n$ die Basisvariablen und $x \in \mathbb{R}^m$ die Nichtbasisvariablen sind. Nehmen wir der Einfachheit halber mal an, dass der Punkt $x = 0$ Element unseres Lösungsbereiches ist. Dann wählen wir diejenige der Nichtbasisvariablen, die zu einer Verbesserung der Zielfunktion führt, und setzen alle anderen Nichtbasisvariablen auf $0$ . Etwas formaler: Finde eine Nichtbasisvariable $x_j$ für die $c_i > 0$ (Man könnte hier selbstverständlich auch die größte auswählen - aber das bringt asymptotisch keine Verbesserung der Laufzeit).

In unserem Beispiel-LP

z = x_1 + 2x_2

unter

\begin{array}{rcrcrcrcl}y_1 &=& 2x_1 &-& 3x_2 &+& 6 &\geq& 0\\y_2 &=& -x_1 &-& 3x_2 &+& 15 &\geq& 0\\y_1 &=& -3x_1 &+& x_2 &+& 15 &\geq& 0 \end{array}

würden wir beispielsweise $x_1$ erhöhen (wobei $x_2 = 0$ ). Nun könnten wir ja theoretisch $x_1$ beliebig hoch setzen, und erhielten dann einen beliebig guten Wert aus unserer Zielfunktion, jedoch würden wir dadurch möglicherweise die Nebenbedingungen verletzen. Das heißt, wir suchen uns diejenige der $n$ Nebenbedingungen heraus, die das Erhöhen der Nichtbasisvariablen am meisten einschränkt.

In unserem Beispiel setzen wir dazu einfach $x_2 = 0$ in die Nebenbedingungen ein, und prüfen welche Bedingung die stärkste Einschränkung an $x_1$ stellt. Also

\begin{array}{rcl}2x_1 + 6 \geq 0 &\Leftrightarrow& x_1 \geq -3 \\ -x_1 + 15 \geq 0 &\Leftrightarrow& x_1 \leq 15 \\ -3x_1 + 15 \geq 0 &\Leftrightarrow& x_1 \leq 5 \end{array}

Die erste Ungleichung stellt keine Einschränkung an $x_1$ , also $x_1$ könnte beliebig wachsen. Die zweite Gleichung fordert dass $x_1$ kleiner als $15$ sein muss, und die Dritte sogar $x_1 \leq 5$ .

Nun haben wir eine Gleichung $i$ gefunden, die unsere Nichtbasisvariable $x_j$ am stärksten einschränkt. Wir führen nun die besagte Koordinatentransformation durch, indem wir die Variablen $y_i$ und $x_j$ „tauschen“. Anschaulich bewegen wir unser Koordinatensystem so, dass die neue Ecke des Polyeders (die in unserem Falle der Punkt $(x_1, x_2) = (3,0)$ ) der neue Ursprung des Koordinatensystems wird. Wenn ihr die Tableau-Notation aus dem Skript benutzt, dann entspricht das gerade dem Austauschalgorithmus mit dem Pivot $(i,j)$ . Was da im Grunde passiert ist nichts anderes, als dass die Gleichung $i$ nach der Variablen $x_j$ aufgelöst wird, und dann für $x_j$ in allen anderen Gleichungen eingesetzt wird. Dadurch wird quasi die Rolle von $y_i$ mit $x_j$ getauscht, denn $x_j$ ist nun links der Gleichheitszeichen, und somit eine Basisvariable, während $y_i$ zu einer Nichtbasisvariablen geworden ist. Wir haben also die Koordinatendarstellung unseres LP geändert!

Machen wir das doch mal für unser Beispiel mit $y_3$ und $x_1$ . Auflösen der Gleichung drei nach $x_1$ führt zu

y_3 = -3x_1 + x_2 +15 \quad \Leftrightarrow \quad x_1 = -\frac13y_3 + \frac13x_2 + 5

und dies eingesetzt für $x_1$ in allen anderen Gleichungen (Zielfunktion nicht vergessen!) ergibt das neue lineare Programm in Normalform:

z = -\frac13y_3 + \frac73x_2 + 5

unter

\begin{array}{rcrcrcrcl}y_1 &=& -2/3y_3 &-& 7/3x_2 &+& 16 &\geq& 0\\y_2 &=& 1/3y_3 &-& 10/3x_2 &+& 10 &\geq& 0\\x_1 &=& -1/3y_3 &+& 1/3x_2 &+& 5 &\geq& 0 \end{array}

Die aktuelle Ecke des Polyeders, die wir jetzt also betrachten ist $(y_3,x_2) = (0,0)$ , und dies entspricht, wenn wir das mal in die Gleichung von $x_1$ einsetzen, dem Punkt $(x_1, x_2) = (5,0)$ – was tatsächlich eine Ecke des Polyeders ist (vgl. graphische Variante im Tut). Außerdem hat sich der Wert der Zielfunktion von $0$ auf $5$ verbessert.

Wir können nun das gleiche Prozedere erneut durchführen. Finde eine Nichtbasisvariable, dessen Erhöhung die Zielfunktion verbessert. Wir könnten beispielsweise $x_2$ nehmen, da diese positiv in der ZF vorkommt. Und so weiter, ich hoffe ihr kommt langsam auf die Idee wie das funktioniert :-).

Wenn es keine verbessernde Nichtbasisvariablen mehr gibt, so sind wir fertig, und haben die optimale Lösung am Punkt $(0,0)$ (natürlich bezüglich der aktuellen Koordinatendarstellung) gefunden. Einsetzen in die entsprechenden Gleichungen $x_1 = \dots$ und $x_2 = \dots$ liefert dann den tatsächlichen Punkt in unserer ursprünglichen Koordinatendarstellung.

Ich hoffe es ist jetzt halbwegs verständlich was der Simplex-Algorithmus in seiner algebraischen Variante macht. In den Lösungen zu den Aufgaben aus dem heutigen Tut habe ich das Beispiel mit dem Rohöl auch nochmal algebraisch durchgeführt.

Verlegung des Tutraums

Samstag, 21.04.2007, 13:21

Auf den Webinscribe-Tutoren-Zetteln stand als Raumangabe für mein Tutorium der Raum -109 im AVG. Leider enthält der Raum keinen Beamer, daher habe ich das Tutorium verlegt, und zwar in den

Raum -109 im Informatik Neubau (Geb. 50.34).

Auf der aktuellen Version der Tutoren-Liste ist das schon korrigiert, aber für alle, die es nicht mehr mitbekommen haben, werde ich am Montag noch ein Goto in den AVG-Raum setzen. :-)

www log₂(n) de

Thomas’ kleine Informatik Seite