Der O-Kalkül, Aufwand von Algorithmen

Hat man einen Algorithmus konstruiert, so möchte man wissen wie schnell oder effizient dieser seine Aufgabe erledigt. Eine Methode, dies zu berechnen, liefert der O-Kalkül.

Hierzu betrachtet man einen Umfang von Eingabedaten (die wir mit nn bezeichnen), und untersuchen wie sich die Laufzeit des Algorithmus verhält wenn man nn stark vergrössert. Konstante Faktoren sind bei dieser Betrachtung nicht von Interesse, da Rechner um konstante Faktoren in ihrer Geschwindigkeit variieren.

Definition

Es gelten folgende Definitionen der Funktionenklassen:

O(g(n)):={f(n)  ∣  ∃c>0,  ∃n0>0:∀n≥n0:0≤f(n)≤c⋅g(n)}o(g(n)):={f(n)  ∣  ∀c>0:∃n0>0:∀n≥n0:0≤f(n)<c⋅g(n)}  Ω(g(n)):={f(n)  ∣  ∃c>0,  ∃n0>0:∀n≥n0:0≤c⋅g(n)≤f(n)}ω(g(n)):={f(n)  ∣  ∀c>0:∃n0>0:∀n≥n0:0≤c⋅g(n)<f(n)}  Θ(g(n)):={f(n)  ∣  ∃c1>0,  ∃c2>0,  ∃n0>0:∀n>n0:0≤c1⋅g(n)≤f(n)≤c2⋅g(n)}\begin{align*} \mathcal{O}(g(n)) &:= \{ f(n) \;|\; \exists c > 0,\; \exists n_0 > 0: \forall n \geq n_0: 0 \leq f(n) \leq c \cdot g(n) \} \\ o(g(n)) &:= \{ f(n) \;|\; \forall c > 0: \exists n_0 > 0: \forall n \geq n_0: 0 \leq f(n) < c \cdot g(n) \} \\\;&\\ \Omega(g(n)) &:= \{f(n) \;|\; \exists c > 0,\; \exists n_0 > 0: \forall n \geq n_0: 0 \leq c \cdot g(n) \leq f(n) \} \\ \omega(g(n)) &:= \{f(n) \;|\; \forall c > 0: \exists n_0 > 0: \forall n \geq n_0: 0 \leq c \cdot g(n) < f(n) \} \\\;&\\ \Theta(g(n)) &:= \{ f(n) \;|\; \exists c_1 > 0,\; \exists c_2 > 0,\; \exists n_0 > 0: \forall n > n_0: 0 \leq c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n) \} \end{align*}

Mit Hilfe dieser Definitionen kann man leicht beschreiben, ob ein Algorithmus f(n)f(n) höchstens (O(g(n)),o(g(n))\mathcal{O}(g(n)), o(g(n))), mindestens (Ω(g(n)),ω(g(n))\Omega(g(n)), \omega(g(n))) oder gleich (Θ(g(n))\Theta(g(n))) stark wie g(n)g(n) wächst.

Abschätzungen

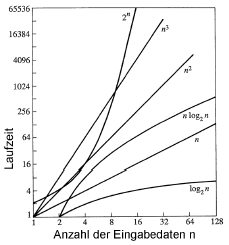
Betrachtet man nun den Aufwand eines Algorithmus, so ist immer der Teil der Ausschlaggebende, der am stärksten wächst; Konstanten werden wie vorher schon gesagt einfach weggelassen. Für einen Algorithmus mit Aufwand T(n)=4n2+16nT(n) = 4n^2 + 16n betrachten wir also nur den n2n^2 Teil. Somit ergeben sich die folgenden, wichtigen Abschätzungen:

Grafik über die Aufwände

O\mathcal{O}-Notation Aufwand
O(1)\mathcal{O}(1) Konstanter Aufwand
O(log⁡2n)\mathcal{O}(\log_2 n) Logarithmischer Aufwand
O(n)\mathcal{O}(n) Linearer Aufwand
O(nlog⁡2n)\mathcal{O}(n \log_2 n) Quasilinearer Aufwand
O(n2)\mathcal{O}(n^2) Quadratischer Aufwand
O(nk)\mathcal{O}(n^k) Polynomialer Aufwand
O(kn)\mathcal{O}(k^n) Exponentieller Aufwand
O(n!)\mathcal{O}(n!) Ganz ganz böse…

Am besten ist natürlich, wenn man es schafft seinen Algorithmus so zu konstruieren, dass er einen Aufwand von O(log⁡n)\mathcal{O}(\log n) hat. Ab O(n2)\mathcal{O}(n^2) wird es ungemütlich, und alles was darüber hinausgeht sollte tunlichst vermieden werden. Um zu illustrieren warum, ist hier eine Tabelle wieviel Daten kk ein Algorithmus einer bestimmten Klasse bei gleichbleibender Zeit verarbeiten kann, wenn die Rechner um den Faktor 1010 schneller werden:

f(n)f(n) g(k)g(k)
log⁡2n\log_2 n 1000⋅k1000 \cdot k
nn 10⋅k10 \cdot k
nlog⁡2nn \log_2 n 99 bis 10⋅k10\cdot k (für große kk)
n2n^2 3⋅k3 \cdot k
2n2^n k+3k + 3
n!n! kk (für k≫10k \gg 10)

Rekurrenzen / Rekursion

Rekurrenzen treten dann auf, wenn ein Algorithmus sich selbst aufruft. Den Aufwand solcher Algorithmen zu bestimmen kann etwas schwieriger sein. Es gibt jedoch eine „Master-Methode“, wenn sich der Aufwand des Algorithmus durch folgende Form beschreiben lässt:

Es seien a≥1a \geq 1, b≥1b \geq 1 und f(n)f(n) eine Funktion. Es sei folgende Rekurrenz gegeben:

T(n)=a⋅T(nb)+f(n)T(n) = a \cdot T(\frac{n}{b}) + f(n)

Dann gelten diese Regeln:

T(n)∈{Θ(nlog⁡b(a)) falls f(n)∈O(nlog⁡b(a)−ε) fu¨r einige ε>0Θ(nlog⁡b(a)⋅log⁡2n) falls f(n)∈Θ(nlog⁡b(a))Θ(f(n)) falls f(n)∈Ω(nlog⁡b(a)+ε)fu¨r einige ε>0 und a⋅f(nb)≤c⋅f(n)fu¨r c<1 und genu¨gend große nT(n) \in \left\{ \begin{array}{lcl} \Theta(n^{\log_b(a)}) & \text{ falls } & f(n) \in \mathcal{O}(n^{\log_b(a) - \varepsilon}) \text{ für einige $\varepsilon > 0$} \\ \Theta(n^{\log_b(a)} \cdot \log_2 n) & \text{ falls } & f(n) \in \Theta(n^{\log_b(a)}) \\ \Theta(f(n)) & \text{ falls } & f(n) \in \Omega(n^{\log_b(a) + \varepsilon}) \\ && \text{für einige $\varepsilon > 0$ und } a \cdot f(\frac{n}{b}) \leq c \cdot f(n) \\&&\text{für $c < 1$ und genügend große $n$} \end{array} \right.

Die meisten Rekurrenzen werden durch diese Methode abgedeckt. Hat man jedoch sehr abgefahrene rekursive Algorithmen, so gibt es noch den allgemeinen Beschleunigungs- und Aufteilungssatz:

Es vermag:

T(n)=∑i=1mT(αi⋅n)+f(n)\displaystyle T(n) = \sum_{i=1}^m T( \alpha_i \cdot n) + f(n) wobei 0<αi<10 < \alpha_i < 1, m≥1m \geq 1, f(n)∈Θ(nk)f(n) \in \Theta(n^k) für k≥1k \geq 1

Dann gilt:

T(n)∈{Θ(nk) falls ∑i=1mαik<1Θ(nklog⁡n) falls ∑i=1mαik=1Θ(nc) falls ∑i=1mαik>1 wobei c bestimmt durch ∑i=1mαic=1T(n) \in \left\{ \begin{array}{lcl} \Theta(n^k) & \text{ falls } & \sum_{i=1}^m \alpha_i^k < 1 \\ \Theta(n^k \log n) & \text{ falls } & \sum_{i=1}^m \alpha_i^k = 1 \\ \Theta(n^c) & \text{ falls } & \sum_{i=1}^m \alpha_i^k > 1 \text{ wobei $c$ bestimmt durch } \sum_{i=1}^m \alpha_i^c = 1 \end{array} \right.

Es sollte klar sein, dass es immernoch Rekurrenzen geben kann, die sich nichtmal mit diesem Satz lösen lassen. Da hilft dann nurnoch raten, oder ein anderes Verfahren (z.B. generierende Funktionen).