• Home
• Theorie
  • Potenzmenge
  • Unendlichkeit der Primzahlen
  • Euler-Formel
  • Diagonalsprache
  • O-Kalkül
  • wp-Kalkül
  • Informationstheorie
  • Schnelle Fourier Transformation
  • Diskrete Kosinus Transformation
• Praxis
  • Huffman Kodierung
  • Primzahlen TM
• Aufschriebe
  • Papers
  • Mathematik
• Tutorien
  • Info III WS05/06
  • Info IV SS06
  • Info III WS06/07
  • Info IV SS07

Die Euler-Formel für Planare Graphen

Ein planarer Graph ist ein Graph der so in die Ebene gezeichnet werden kann, dass sich keine zwei Kanten überschneiden. Die Kanten dürfen dabei durchaus beliebige Jordankurven sein. Neben den Knoten und Kanten, die den Graphen definieren, lässt sich für planare Graphen auch der Begriff der Facette definieren. Eine Facette ist ein durch Kanten begrenztes Gebiet in der Zeichnung des Graphen. Der Bereich außerhalb des Graphen zählt auch als Facette, und wird meist als äußere Facette bezeichnet. Beispielsweise lässt sich der dreidimensionale Würfel so in die Ebene einbetten, dass sich keine Kanten überkreuzen.

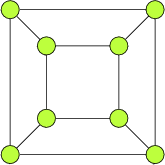
Man zählt 8 Knoten, 12 Kanten und 6 Facetten.

Die Eulersche Formel bringt nun für beliebige planare Graphen die Anzahl der Facetten, Kanten und Knoten in eine mathematische Beziehung. Sie besagt, dass für einen planaren und zusammenhängenden Graphen mit $n$ Knoten, $m$ Kanten und $f$ Facetten gilt:

$$n - m + f = 2$$

Für diese schlichte Formel gibt es einen äußerst eleganten und kurzen Beweis, der im Gegensatz zum kanonischen Beweis, ganz ohne Induktion auskommt!

Beweis

Wir betrachten eine beliebige Einbettung des Graphen $G$ in der Ebene. Ist $G$ zusammenhängend, so gilt das auch für den dualen Graphen $G^*$. Nach dem Satz von Jordan, induziert eine Menge von Kreisen in $G$ einen Schnitt in $G^*$ und umgekehrt ein Schnitt in $G$ eine Menge von Kreisen in $G^*$.

Wir betrachten nun einen aufspannenden Baum $T$ in $G$, sowie den dualen Graphen $T^* := (G \setminus T)^*$, also zu dem durch die Nichtbaumkanten induzierten Subgraph in $G$. Natürlich ist $T^*$ ein Subgraph von $G^*$. Weiterhin entspricht jede Kante in $T^*$ einer Nichtbaumkante in $G$, so dass $|E_G| = |E_{T^*}| + |E_{T}|$ gilt. Aus dem Satz von Jordan lässt sich außerdem folgern, dass $T^*$ sogar ein aufspannender Baum in $G^*$ ist, was gleichbedeutend mit $|V_{T^*}| = |V_{G^*}| = |F_{G}|$ ist.

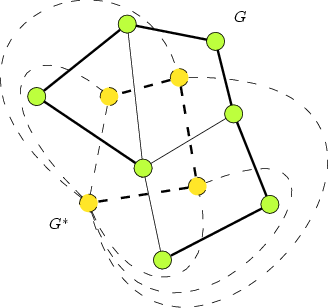
Da ein Baum mit $k$ Knoten genau $k-1$ Kanten enthält, folgt aus den obigen Beobachtungen

$$(\underbrace{|V_G|}_{= n} - 1) + (\underbrace{|V_{T^*}|}_{= f} - 1) = \underbrace{E_G}_{= m} \quad \Longleftrightarrow \quad n - m + f = 2$$

Fertig! $\square$