Informationstheorie nach Shannon

Die Informationstheorie, die von Claude Shannon in den 40er/50er Jahren entwickelt wurde, stellt ein Maß bzw. Kalkül zur Verfügung den Begriff “Information” und “Informationsgehalt” zu quantisieren um damit rechnen zu können.

Vorbemerkungen

In der Informationstheorie betrachten wir stets Quellen die Zeichen aussenden. Die Menge aller möglichen Zeichen die auftreten können heißt Alphabet und wird in der Regel mit XX bezeichnet. Ein Beobachter, der die Zeichenquelle betrachtet möchte nun wissen, welche „Information“ in den Zeichen steckt, die die Quelle aussendet.

Um dies zu modellieren bedient man sich der Wahrscheinlichkeitstheorie. Man definiert eine Wahrscheinlichkeitsverteilung auf dem Alphabet. Man weiß dadurch mit welcher Wahrscheinlichkeit welches Zeichen ausgesendet wird. Zum Beispiel sendet eine Quelle die Zeichenkette SS:

X:={0,1}undS:=00111101101101.X := \{0,1\} \quad \text{und} \quad S := 00111101101101.

Nachzählen ergibt also, dass wir insgesamt 14 Zeichen bekommen haben und davon 5 Mal die 0 und 9 Mal die 1. Das heißt unsere Wahrscheinlichkeitsverteilung ist

P(0)=514undP(1)=914.P(0) = \frac{5}{14} \quad \text{und} \quad P(1) = \frac{9}{14}.

Die Information

Wie bringen wir nun die Information herein? Shannon definierte die Information II, die ein Zeichen xi∈Xx_i \in X enthält durch

I(xi)=−log⁡2(P(X=xi))I(x_i) = - \log_2(P(X = x_i))

Die Einheit der Information ist bit. Man beachte, dass dies eine reelle Zahl sein kann (und meistens auch ist), und daher nicht mit dem normal üblichen Bit (Großgeschrieben) zu verwechseln ist!

Es ist also gerade der negative Logarithmus über die relative Auftrittswahrscheinlichkeit des Zeichens xix_i! Das macht auch Sinn, denn der Logarithmus ist zwischen 0 und 1 immer negativ, und eine relative Wahrscheinlichkeit ist stets im Bereich 0 bis 1. Somit ist die Information eines Zeichens xix_i stets größer als 0.

Für unser Beispiel ausgerechnet ist demnach

I(0)=−log⁡2514≈1,485426827 bitI(0) = - \log_2 \frac{5}{14} \approx 1{,}485426827\,\text{bit}

und

I(1)=−log⁡2914≈0,6374299205 bit.I(1) = - \log_2 \frac{9}{14} \approx 0{,}6374299205\,\text{bit}.

Warum ist die Information von 0 höher? Weil sie seltener vorkommt. Wenn die Quelle eine 11 ausspuckt ist das weitaus weniger „überraschend“. Man würde eine 11 also eher erwarten, und erhält damit weniger Information, als wenn eine 00 kommt, da diese verhältnismäßig selten vorkommen.

Durchschnittlicher Informationsgehalt aka „Entropie“

Mit der oberen Formel können wir nun den Informationsgehalt eines Zeichens schön berechnen. Nun möchte man aber vielleicht wissen wieviel Information ein Zeichen in einer Zeichenkette „im Mittel“ enthält. Aus der Wahrscheinlichkeit weiß man, dass dies gerade der Erwartungswert der statistischen Variable – in unserem Fall also XX – ist. Also

E=∑iP(X=xi)xi.E = \sum_{i} P(X = x_i) x_i.

Übertragen wir das auf die Informationstheorie. Wir können für jedes Zeichen xix_i ja die Einzelinformationen berechnen. Nun bilden wir einfach den Erwartungswert und das liefert die Formel für die Entropie

H=∑iP(X=xi)I(xi)H = \sum_i P(X = x_i) I(x_i)

Wir können das noch etwas vereinfach, nämlich

H=∑iP(X=xi)I(xi)=∑iP(X=xi)(−log⁡2(P(X=xi)))=−∑iP(X=xi)log⁡2(P(X=xi))=−∑iPilog⁡2(Pi)(Kurzschreibweise)\begin{align*} H &= \sum_i P(X=x_i) I(x_i) \\ &= \sum_i P(X=x_i) (- \log_2 (P(X=x_i))) \\ &= - \sum_i P(X=x_i) \log_2 (P(X=x_i)) \\ &= - \sum_i P_i \log_2(P_i) \quad \text{(Kurzschreibweise)} \end{align*}

Anschaulich ist dies also der durchschnittliche Informationsgehalt eines Zeichens; Und zwar der Zeichen, die die Quelle ausspuckt.

Man notiert auch – analog zur Wahrscheinlichkeitstheorie – die Entropie HH durch H(P1,…,Pk)H(P_1, \ldots, P_k). Wichtig ist dabei, dass die Wahrscheinlichkeiten PiP_i aufsummiert gerade 1 ergeben, da der Wert HH sonst illegal ist, bzw. überhaupt keinen Sinn ergibt.

Unser Beispiel von oben mit der Zeichenkette SS liefert nun eingesetzt in die Formel

H=−514log⁡2(514)−914log⁡2(914)≈0,9402859585 bit.H = - \frac{5}{14} \log_2 \left(\frac{5}{14}\right) - \frac{9}{14} \log_2 \left(\frac{9}{14}\right) \approx 0{,}9402859585\,\text{bit}.

Dies ist also die Entropie, also der durchschnittliche Informationsgehalt pro Zeichen der Zeichenkette SS.

Wollten wir den Informationsgehalt der kompletten Zeichenkette, so müssen wir unser HH noch mit der Länge der Zeichenkette multiplizieren, also

HS=∣S∣⋅H≈14⋅0,9402859585≈13,16400342 bit.H_{S} = |S| \cdot H \approx 14 \cdot 0{,}9402859585 \approx 13{,}16400342\,\text{bit}.

Die Zeichenkette SS enthält also eine Information von ungefähr 13 bit!

Der Kanal

Man möchte nun noch einen Schritt weiter gehen und betrachtet nicht nur die Information von Zeichenketten die eine Quelle ausspuckt, sondern man betrachtet einen Übetragungskanal durch den wir einen Datenstrom schicken wollen. Wir brauchen also jetzt zwei Alphabete XX und YY, nämlich die des Senders und die des Empfängers.

Nun kann es passieren, dass der Kanal gestört wird, das heißt Informationen des Senders verloren gehen, oder ungewollte Informationen hinzukommen. Die Quelle wird also in der Regel nicht das gleiche Empfangen was der Sender ausgespuckt hat. Schematisch kann man das am folgenden Bild illustrieren:

Schema

Keine Panik, das Bild ist schnell erklärt!

Die Quelle (links) sendet Zeichen aus einem Alphabet XX in den Kanal. Die Quelle empfängt irgendwelche Zeichen aus YY vom Kanal. Hier muss man jetzt ein wenig aufpassen. Es können in der Praxis XX und YY die gleichen Alphabete sein, aber es sind trotzdem verschiedene stochastische Variablen! Der Anteil von Information, der an der Quelle ankommt und tatsächlich vom Sender stammt heißt Transinformation. Der verlorengegangene Anteil an Information von der Quelle heißt auch Äquivokation und der hinzugekommene Anteil heißt Fehlinformation. Man kann sich aus dem Diagramm jetzt wunderbar folgende Beziehungen herleiten:

Transinformation:

H(X;Y):=H(X)−H(X∣Y)=H(Y)−H(Y∣X)H(X;Y) := H(X) - H(X|Y) = H(Y) - H(Y|X)

Äquivokation:

H(X∣Y):=H(X)−H(X;Y)H(X|Y) := H(X) - H(X;Y)

Fehlinformation (Irrelevanz):

H(Y∣X):=H(Y)−H(X;Y)H(Y|X) := H(Y) - H(X;Y)

Totalinformation:

H(X,Y):=H(X∣Y)+H(X;Y)+H(Y∣X)H(X,Y) := H(X|Y) + H(X;Y) + H(Y|X)

Diese Formeln lassen sich natürlich auch (durch ineinander Einsetzen bzw. anderes Ablesen aus dem Diagramm) anders formulieren.

OK, schlagen wir wieder einen Bogen zur Wahrscheinlichkeitstheorie. Man kann XX und YY wieder als Zufallsvariablen ansehen. Diese sind in der regel stochastisch Abhängig, außer der Sender hat mit der Quelle nichts am Hut, aber was wär das für ein Kanal? Betrachten wir die Verbundwahrscheinlichkeit stochastisch Abhängiger Größen einmal genauer im Vergleich zu den Informationsgehalten

P(X,Y)=P(Y∣X)⋅P(X)↔H(X,Y)=H(Y∣X)+H(X).P(X,Y) = P(Y|X) \cdot P(X) \quad \leftrightarrow \quad H(X,Y) = H(Y|X) + H(X).

Diese Beziehung sollte man stets im Kopf behalten. Es gilt: Ein Produkt der Wahrscheinlichkeiten entspricht einer Summation der Entropien, was aus der isomorphen Beziehung zwischen der Multiplikation reeller Zahlen und der Summierung ihrer Logarithmen herrührt.

Nun gibt es noch ein paar Eigenschaften von Kanälen:

Deterministischer Kanal

Ein Kanal heißt deterministisch, wenn für jedes Eingabezeichen klar ist, was deren Ausgabezeichen sein wird. Es muss also gelten H(Y∣X)=0H(Y\vert{}X) = 0, es darf keine Fehlinformation geben!

Verlustfreier Kanal

Ein Kanal heißt verlustfrei, wenn es keine Äquivokation (verlorene Information) gibt, also H(X∣Y)=0H(X\vert{}Y) = 0 gilt.

Störungsfreier Kanal

Ein Kanal heißt störungsfrei (oder ungestört), wenn er verlustfrei und deterministisch ist.

Nutzloser Kanal

Ein Kanal heißt nutzlos wenn er keine Information überträgt, bzw. wenn gilt H(X;Y)=0H(X;Y) = 0. In diesem Fall sind die Zufallsvariablen für XX und YY stochastisch unabhängig.

Schließlich gibt es noch eine Größe, die angibt wieviel Information man maximal durch einen Kanal schicken kann, die sogenannte Kanalkapazität. Diese ist definiert durch

C=max⁡P(X)(H(X;Y))C = \max_{P(X)}(H(X;Y))

Anschaulich ist dies also unter allen möglichen Wahrscheinlichkeitsverteilungen der Quelle diejenige zugehörige Transinformation, die am größten ist.

Definition von Kanälen

OK, genug der trockenen Theorie. Wie definiert man im Allgemeinen einen Kanal? Eine Möglichkeit ist zum Beispiel durch Angabe der bedingten Wahrscheinlichkeiten P(Y∣X)P(Y|X). Sowas könnte zum Beispiel für einen Kanal mit X={0,1}X = \{0,1\} und Y={0,1}Y = \{0,1\} so aussehen:

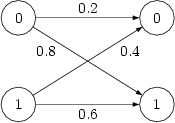
Beispiel

Links haben wir XX und rechts YY. Die Pfeile geben die bedingte Wahrscheinlichkeit P(Y=y∣X=x)P(Y=y | X=x) an. Hat man nun noch eine passende Quellenstatistik gegeben, zum Beispiel

P(X=0):=12P(X=1):=12,P(X = 0) := \frac{1}{2} \qquad P(X=1) := \frac{1}{2},

so lassen sich alle Größen des Kanals berechnen. Folgende Größen lassen sich direkt berechnen:

Informationsgehalt der Qelle

H(X)=H(P(X=x1),…,P(X=xn))H(X) = H(P(X=x_1), \ldots, P(X=x_n))

Informationsgehalt des Empfängers

H(Y)=H(P(Y=y0),…,P(Y=yn))H(Y) = H(P(Y=y_0), \ldots, P(Y=y_n))

Totalinformation

H(X,Y)=  H(P(X=x0)P(Y=y0∣X=x0),…,P(X=x0)P(Y=yn∣X=x0),…,…,P(X=xn)P(Y=yn∣X=xn))\begin{align*} H(X,Y) =\;&H(P(X=x_0)P(Y=y_0|X=x_0), \ldots, P(X=x_0)P(Y=y_n|X=x_0), \ldots,\\& \ldots, P(X=x_n)P(Y=y_n|X=x_n)) \end{align*}

Die restlichen Größen lassen sich mit den Beziehungen aus dem Diagramm leicht herleiten. Für unser Beispiel ergibt sich die Quelleninformation durch:

H(X)=H(P(X=0),P(X=1))=H(12,12)=−12log⁡212−12log⁡212=1 bit\begin{align*} H(X) &= H(P(X=0), P(X=1)) \\ &= H(\frac{1}{2},\frac{1}{2}) \\ &= - \frac{1}{2} \log_2\frac{1}{2} - \frac{1}{2} \log_2 \frac{1}{2} \\ &= 1 \text{ bit} \end{align*}

Die Information H(Y)H(Y) lässt sich auch berechnen:

H(Y)=H(P(Y=0),P(Y=1))=H(12⋅0,2+12⋅0,4,12⋅0,8+12⋅0,6)=H(0,3,0,7)≈0,88 bit\begin{align*} H(Y) &= H(P(Y=0), P(Y=1)) \\ &= H(\frac{1}{2} \cdot 0{,}2 + \frac{1}{2} \cdot 0{,}4, \frac{1}{2} \cdot 0{,}8 + \frac{1}{2} \cdot 0{,}6) \\ &= H(0{,}3, 0{,}7) \\ &\approx 0{,}88 \text{ bit} \end{align*}

Und schließlich H(X,Y)H(X,Y):

H(X,Y)=H(P(X=0)P(Y=0∣X=0),P(X=0)P(Y=1∣X=0),P(X=1)P(Y=0∣X=1),P(X=1)P(Y=1∣X=1))=H(12⋅0,2,12⋅0,8,12⋅0,4,12⋅0,6)=H(0,1,0,2,0,4,0,3)≈1,85 bit\begin{align*} H(X,Y) &= H(P(X=0)P(Y=0|X=0), P(X=0)P(Y=1|X=0),\\&\qquad P(X=1)P(Y=0|X=1), P(X=1)P(Y=1|X=1)) \\ &= H(\frac{1}{2} \cdot 0{,}2, \frac{1}{2} \cdot 0{,}8, \frac{1}{2} \cdot 0{,}4, \frac{1}{2} \cdot 0{,}6) \\ &= H(0{,}1, 0{,}2, 0{,}4, 0{,}3) \\ &\approx 1{,}85 \text{ bit} \end{align*}

Die restlichen Werte lassen sich durch die oberen Formeln ausrechnen, in unserem Fall:

H(X∣Y)=H(X,Y)−H(Y)≈0,97 bitH(Y∣X)=H(X,Y)−H(X)≈0,84 bitH(X;Y)=H(X)−H(X∣Y)≈0,03 bit\begin{align*} H(X|Y) &= H(X,Y) - H(Y) \approx 0{,}97 \text{ bit}\\ H(Y|X) &= H(X,Y) - H(X) \approx 0{,}84 \text{ bit}\\ H(X;Y) &= H(X) - H(X|Y) \approx 0{,}03 \text{ bit} \end{align*}

Die Transinformation, also die Information, die der Kanal wirklich überträgt ist mit 0.03 bit in unserem Beispiel leider extrem gering.

Redundanz

Redundanz bezeichnet in der Informationstheorie „überflüssige Information“. Diese kommt dann zustande, wenn man einen Text mit mehr Bits kodiert, als eigentlich nötig, also mehr als die enthaltene Information des Textes.

Definieren wir zunächst einmal die tatsächliche Anzahl bits. Wir haben also wieder ein Alphabet XX mit Zeichen xi∈Xx_i \in X. Dann bezeichnet code(xi)\text{code}(x_i) das zu xix_i gehörende Kodewort. Zum Beispiel beim Alphabet der ASCII-Zeichen hat der Buchstabe aa das Kodewort 0110000101100001, also code(a)=01100001\text{code}(a) = 01100001. Analog zur Entropie HH, die ein Erwartungswert über die Information der Zeichen ist, ist die Nominalinformation H~\tilde{H} als Erwartungswert über die Kodewortlänge definiert:

H~=∑iP(X=xi)⋅∣code(xi)∣\tilde{H} = \sum_{i} P(X=x_i) \cdot |\text{code}(x_i)|

Diese ist quasi die „durchschnittliche Kodewortlänge pro Zeichen“.

Wir haben nun also zwei Größen, die wir gegenüberstellen können, nämlich die tatsächliche Kodelänge (H~\tilde{H}) und die eigentlich bloß benötigte Kodelänge aufgrund der Information (HH). Damit ist die absolute Redundanz RabsR_{\text{abs}} folgendermaßen definiert

Rabs=H~−HR_{\text{abs}} = \tilde{H} - H

Die relative Redundanz ist dementsprechend ein Wert zwischen 0 und 1 und ist

Rrel=RabsH~=1−HH~R_{\text{rel}} = \frac{R_{\text{abs}}}{\tilde{H}} = 1 - \frac{H}{\tilde{H}}

Ein kleines Beispiel. Betrachten wir die Zeichenkette „Hallo“. Offenbar ist das Alphabet X={H,a,l,o}X = \{H,a,l,o\}. Die Wahrscheinlichkeitsverteilung ergibt sich durch nachzählen und ist

P(X=H)=15P(X=a)=15P(X=l)=25P(X=o)=15P(X=H) = \frac{1}{5} \quad P(X=a) = \frac{1}{5} \quad P(X=l) = \frac{2}{5} \quad P(X=o) = \frac{1}{5}

Damit können wir die Entropie HH berechnen

H=H(15,15,25,15)=−3⋅(15log⁡215)−(25log⁡225)≈1.92 bit\begin{align*} H &= H(\frac{1}{5}, \frac{1}{5}, \frac{2}{5}, \frac{1}{5}) \\ &= - 3 \cdot (\frac{1}{5} \log_2 \frac{1}{5}) - (\frac{2}{5} \log_2 \frac{2}{5}) \\ &\approx 1.92 \text{ bit} \end{align*}

Da bei der ASCII-Kodierung jedes Zeichen durch 8 Bit repräsentiert wird, können wir H~=8\tilde{H} = 8 setzen. Somit ergibt sich eine absolute Redundanz von

Rabs≈8−1,92=6,08 bitR_{\text{abs}} \approx 8 - 1{,}92 = 6{,}08\,\text{bit}

und eine relative Redundanz von

Rrel≈1−1,928=0,76 =^ 76 %.R_{\text{rel}} \approx 1 - \frac{1{,}92}{8} = 0{,}76\ \hat{=}\ 76\,\%.

Um die Information, die die Zeichenkette „Hallo“ enthält zu Kodieren, reichen also 1.92 bit pro Zeichen aus. Im ASCII-Kode sind also pro Zeichen 6.08 bit (76%) „überflüssig“.

Maximale und minimale Information

Sehr interessant ist noch, dass der Informationsgehalt (Entropie) zu einer Zufallsvariable (und einem Alphabet) XX dann maximal wird, wenn auf dem Alphabet eine Gleichverteilung vorliegt. Intuitiv ist das klar, denn bei einer Gleichverteilung der Zeichen weiß man am wenigsten welches Zeichen als nächstes auftreten wird, daher wird jedes eine hohe Information mitbringen.

Der Informationsgehalt wird im Gegenzug dann minimal, wenn die Wahrscheinlichkeitsverteilung so aussieht, dass ein Zeichen xix_i eine Auftrittswahrscheinlichkeit von 100% besitzt. Die restlichen Zeichen haben dann natürlich eine Auftrittswahrscheinlichkeit von 0. Dann bringt ein Auftauchen von xix_i nämlich überhaupt keine Information mit, da man ja eh schon wusste dass xix_i kommt.