Schnelle Fourier Transformation (FFT)

Die schnelle Fourier Transformation (engl. Fast Fourier Transform, FFT) ist in der Informatik (besonders in der Signalverarbeitung) ein sehr wichtiger Algorithmus zur schnellen Berechnung der diskreten Fourier Transformation (DFT). Um die FFT zu erklären muss vorher noch ein Wenig über die DFT gesagt werden. Ich setze in diesem Artikel außerdem grundlegende Kenntnisse der komplexen Zahlen C\mathbb{C} voraus.

Diskrete Fourier Transformation

Die diskrete Fourier Transformation ist sehr schnell erklärt (wenn man sie nicht von der allgemeinen Fourier Transformation herleitet). Sie ist eine Abbildung f^:Cn→Cn\hat{f}: \mathbb{C}^n \to \mathbb{C}^n. Sie bildet also komplexe Vektoren auf komplexe Vektoren ab. Wir definieren uns zunächst

ω:=e2iπn=cos⁡2πn+isin⁡2πnNach der Eulerschen Identita¨t\begin{align*} \omega &:= e^{\frac{2 i \pi}{n}} \\ &= \cos \frac{2\pi}{n} + i \sin \frac{2\pi}{n} \quad \text{Nach der Eulerschen Identität} \end{align*}

Man nennt ω\omega auch die primitive n-te Einheitswurzel. Zur Erinnerung: nn ist die Länge unseres „Eingabevektors“. OK, jetzt definieren wir uns noch eine Matrix FF. Dies geschieht ganz einfach:

Fkl:=wk⋅lk,l=0…n−1F_{kl} := w^{k \cdot l} \qquad k,l = 0 \ldots n-1

Wir nennen FF die Fouriermatrix. Anders gesprochen ist dies gerade die Vandermonde-Matrix V(ω0,ω1,…,ωn−1)V(\omega^0, \omega^1, \ldots, \omega^{n-1}), aber das ist erstmal egal.

Schließlich definieren wir uns die diskrete Fourier Transformation. Haben wir einen Vektor x∈Cnx \in \mathbb{C}^n, so ist die Fourier Transformation f^:Cn→Cn\hat{f}: \mathbb{C}^n \to \mathbb{C}^n definiert durch

f^(x):=F⋅x\hat{f}(x) := F \cdot x

Sie ist also nichts weiter als eine Matrix-Vektor-Multiplikation der Fouriermatrix mit dem Vektor xx. In der Literatur findet man auch oft die Formel

f^(x)p=∑k=0n−1e2iπn⋅k⋅p⋅xp=∑k=0n−1ωkp⋅xp=∑k=0n−1Fkp⋅xp \begin{align*} \hat{f}(x)_p &= \sum_{k=0}^{n-1} e^{\frac{2 i \pi}{n} \cdot k \cdot p} \cdot x_p \\ &= \sum_{k=0}^{n-1} \omega^{kp} \cdot x_p \\ &= \sum_{k=0}^{n-1} F_{kp} \cdot x_p \> \end{align*}

Man sieht, dies ist nichts anderes als die ausgeschriebene Matrix-Vektor-Multiplikation.

Beispiel

Wie sieht sowas aus? Sagen wir, wir wollen den Vektor x=(1234)x = \left(\begin{smallmatrix}1\\2\\3\\4\end{smallmatrix}\right) transformieren. Es ist also n=4n = 4. Die 4-te primitive Einheitswurzel ist ω=e2iπ4=i\omega = e^{\frac{2 i \pi}{4}} = i. Konstruktion der Fouriermatrix ergibt

F=(11111i−1−i1−11−11−i−1i)F = \begin{pmatrix}1&1&1&1\\1&i&-1&-i\\1&-1&1&-1\\1&-i&-1&i\end{pmatrix}

Die Rechnung F⋅xF \cdot x ist nun wirklich trivial und es ist f^(x)=(10−2−2i−2−2+2i)\hat{f}(x) = \left(\begin{smallmatrix}10\\-2 - 2i\\-2\\-2+2i\end{smallmatrix}\right). Dies ist schon unser transformierter Vektor!

Inverse Diskrete Fourier Transformation

Jetzt stellt sich die Frage wie wir den Vektor f^\hat{f} wieder zurücktransformiert bekommen. Klar dürfte sein, dass eine Multiplikation mit der inversen Fouriermatrix F−1F^{-1} wieder den ursprünglichen Vektor liefern wird. Aufgrund der Eigenschaften der primitiven Einheitswurzeln und der Symmetrie von FF ist die Inverse Matrix F−1F^{-1} gegeben durch

Fkl−1=1n⋅Fkl‾=1nω−k⋅lF^{-1}_{kl} = \frac{1}{n} \cdot \overline{F_{kl}} = \frac{1}{n} \omega^{-k \cdot l}

Dabei bezeichnet Fkl‾\overline{F_{kl}} die konjugiert komplexe Zahl von FklF_{kl}. Die Rücktransformation ist also nun auch wieder nur eine Matrix-Vektor-Multiplikation, nämlich

f^−1(x^)=F−1⋅x^\displaystyle\hat{f}^{-1}(\hat{x}) = F^{-1} \cdot \hat{x}

That’s it! In unserem Beispiel von oben wechseln wir in der Matrix FF einfach das Vorzeichen vor dem Imaginärteil jeder komplexen Zahl, und ziehen 1n=14\frac{1}{n} = \frac{1}{4} vor die Matrix und erhalten

F−1=14⋅(11111−i−1i1−11−11i−1−i)F^{-1} = \frac{1}{4} \cdot \begin{pmatrix}1&1&1&1\\1&-i&-1&i\\1&-1&1&-1\\1&i&-1&-i\end{pmatrix}

womit dann F−1⋅(10−2−2i−2−2+2i)=(1234)F^{-1} \cdot \left(\begin{smallmatrix}10\\-2 - 2i\\-2\\-2+2i\end{smallmatrix}\right) = \left(\begin{smallmatrix}1\\2\\3\\4\end{smallmatrix}\right) folgt.

Schnelle Fourier Transformation

Die Schnelle Fourier Transformation ist ein Teile & Herrsche Algorithmus zur Berechnung der DFT. Im O-Kalkül ergibt sich, dass die DFT wegen der Matrix-Vektor-Multiplikationen einen Aufwand von O(n2)\mathcal{O}(n^2) hat. Der Algorithmus der FFT schafft die gleichen Berechnungen in O(nlog⁡n)\mathcal{O}(n \log n), was eine wesentliche Verbesserung darstellt! Kleiner Haken an der Sache ist jedoch, dass die Länge der zu transformierenden Vektoren eine Zweierpotenz sein muss. In den meisten Fällen ist das aber egal, da man einfach den Vektor mit Nullen auffüllen kann bis seine Länge gerade die einer Zweierpotenz entspricht.

Das Verfahren

Wie schon angesprochen handelt es sich bei der FFT um einen Teile & Herrsche Algorithmus, welcher sich am einfachsten rekursiv formulieren lässt. Wir möchten also den transformierten Vektor b=F⋅ab = F \cdot a berechnen. Dabei sind a=(a1,a2,…,a2m)a = (a_1, a_2, \ldots, a_{2^m}) und b=(b1,b2,…,b2m)b = (b_1, b_2, \ldots, b_{2^m}) mit m∈Nm \in \mathbb{N}. Wir können den Vektor bb also aufspalten, und zwar in die Vektoren b(g)b^{(g)}, der gerade die Komponenten von bb mit geradem Index und b(u)b^{(u)} der die Komponenten von bb mit ungeradem Index enthält. Ausgeschrieben heißt das für b(g)b^{(g)}

bk(g)=b2k=∑l=0n−1ωl(2k)al=∑l=0n2−1wl(2k)al+∑l=0n2−1ω(n2+l)2kan2+l=∑l=0n2−1wl(2k)(al+an2+l)\begin{align*} b_k^{(g)} &= b_{2k}\\ &= \sum_{l=0}^{n-1} \omega^{l(2k)} a_l \\ &= \sum_{l=0}^{\frac{n}{2} - 1} w^{l(2k)} a_l + \sum_{l=0}^{\frac{n}{2}-1} \omega^{(\frac{n}{2} + l) 2k} a_{\frac{n}{2} + l} \\ &= \sum_{l=0}^{\frac{n}{2} - 1} w^{l(2k)} (a_l + a_{\frac{n}{2} + l}) \end{align*}

Uff, was wurde hier gemacht? Zunächst einmal berechnen sich die geraden Komponenten von bb ja dadurch, dass wir die geraden Zeilen der Matrix FF mit aa multiplizieren. Dies lässt sich als Summe schreiben. Die Summe können wir in der Mitte teilen und erhalten damit die dritte Zeile. Jetzt nutzen wir aus, dass ω\omega eine primitive Einheitswurzel ist. Dann gilt nämlich

ω(n2+l)2k=ωnk+l(2k)=ωl(2k)⋅ωnk=ωl(2k)⋅ei2πnkn=ωl(2k)⋅ei(2πk)=ωl(2k)⋅(cos⁡(2kπ)⏟=1+isin⁡(2kπ)⏟=0)=ωl(2k)\begin{align*} \omega^{(\frac{n}{2} + l) 2k} &= \omega^{nk + l(2k)} \\ &= \omega^{l(2k)} \cdot \omega^{nk} \\ &= \omega^{l(2k)} \cdot e^{i \frac{2\pi nk}{n}} \\ &= \omega^{l(2k)} \cdot e^{i (2\pi k)} \\ &= \omega^{l(2k)} \cdot ( \underbrace{\cos (2k \pi)}_{= 1} + i \underbrace{\sin (2k \pi)}_{= 0})\\ &= \omega^{l(2k)} \end{align*}

Damit kann man also die Summe zusammenziehen (wie oben in der letzten Zeile gezeigt)! Substituiere nun m=n2m = \frac{n}{2} und ν=ω2\nu = \omega^2 (ν\nu ist also m-te primitive Einheitswurzel) und wir erhalten

bk(g)=∑l=0m−1νlk(al+am+l)b_k^{(g)} = \sum_{l=0}^{m - 1} \nu^{lk} (a_l + a_{m+l})

Das ist also nichts anderes als die Fouriertransformation des Vektors (a0+am⋮am−1+an−1)\left(\begin{smallmatrix}a_0 + a_{m} \\ \vdots \\ a_{m-1} + a_{n-1} \end{smallmatrix}\right). Der Vektor hat gerade die Länge n2=m\frac{n}{2} = m.

Machen wir das gleiche Spiel mit den ungeraden Indizes von bb:

bk(u)=b2k+1=∑l=0n−1ωl(2k+1)al=∑l=0n2−1wl(2k+1)al+∑l=0n2−1ω(n2+l)(2k+1)an2+l=∑l=0n2−1ωlwl(2k)al+∑l=0n2−1−ωlωl(2k)an2+l=∑l=0n−1ωl(2k)ωl(al−an2+l)\begin{align*} b_k^{(u)} &= b_{2k+1} \\ &= \sum_{l=0}^{n-1} \omega^{l(2k+1)} a_l \\ &= \sum_{l=0}^{\frac{n}{2} - 1} w^{l(2k+1)} a_l + \sum_{l=0}^{\frac{n}{2}-1} \omega^{(\frac{n}{2} + l)(2k+1)} a_{\frac{n}{2}+l} \\ &= \sum_{l=0}^{\frac{n}{2} - 1} \omega^l w^{l(2k)} a_l + \sum_{l=0}^{\frac{n}{2}-1} - \omega^l \omega^{l(2k)} a_{\frac{n}{2}+l} \\ &= \sum_{l=0}^{n-1} \omega^{l(2k)} \omega^l (a_l - a_{\frac{n}{2} + l}) \end{align*}

Die Umformungen von Zeile 3 nach 4 in der rechten Summe ausführlich:

ω(n2+l)(2k+1)an2+l=ωnk+n2+l(2k)+l=ωnk⏟=1ωn2ωl(2k)ωl=eiπωl(2k)ωl=(cosπ⏟=−1+isin⁡π⏟=0)ωl(2k)ωl=−ωl(2k)ωl\begin{align*} \omega^{(\frac{n}{2} + l)(2k+1)} a_{\frac{n}{2}+l} &= \omega^{nk + \frac{n}{2} + l(2k) + l}\\ &= \underbrace{\omega^{nk}}_{= 1} \omega^{\frac{n}{2}} \omega^{l(2k)}\omega^l\\ &= e^{i \pi} \omega^{l(2k)} \omega^l \\ &= (\underbrace{cos \pi}_{= -1} + i \underbrace{\sin \pi}_{=0}) \omega^{l(2k)} \omega^{l} \\ &= - \omega^{l(2k)} \omega^{l} \end{align*}

Ok, wir können also wieder m=n2m = \frac{n}{2} und ν=ω2\nu = \omega^2 substituieren und erhalten

bk(u)=∑l=0m−1νlkωl(al−am+l)b_k^{(u)} = \sum_{l=0}^{m-1} \nu^{lk} \omega^l (a_l - a_{m+l})

Wieder ist dies nichts anderes als die Fouriertransformation des Vektors (ω0(a0−am)⋮ωm−1(am−1−an−1))\left(\begin{smallmatrix}\omega^0(a_0 - a_{m}) \\ \vdots \\ \omega^{m-1}(a_{m-1} - a_{n-1}) \end{smallmatrix}\right).

Diese Zerlegung lässt sich jetzt rekursiv weiter durchführen bis wir Vektoren der Länge 1 haben. Die Fouriertransformierte eines Vektors der Länge 1 ist jedoch der Vektor selbst (Es gilt ja bei n=1n = 1 dass F=(1)F = (1) ist), somit haben wir auch eine rekursive „Abbruchbedingung“.

Zusammengefasst geht man also so vor:

Dieses Verfahren hat nun eine Komplexität von nurnoch O(nlog⁡n)\mathcal{O}(n \log n)!

Inverse Schnelle Fourier Transformation

Die Umkehrung der FFT ist wieder eine FFT. Wie wir jedoch im Kapitel der DFT gesehen haben muss diesmal die Matrix F−1F^{-1} benutzt werden. Wir benutzen also die konjugiert komplexen Einheitswurzeln ω‾\overline{\omega} statt ω\omega und müssen die Endergebnisse noch mit 1n\frac{1}{n} multiplizieren. Aufwand: Wieder O(nlog⁡n)\mathcal{O}(n \log n).

Das Butterfly Schema

Das oben angegebene Verfahren lässt sich algorithmisch sehr schön implementieren, aber will man die FFT auf dem Papier durchführen ist es etwas umständlich, da man viele temporäre Vektoren ausrechnen muss. Abhilfe schafft da das hochbedenkliche Butterfly Schema. Als Butterfly bezeichnet man einen Graph bei dem jeder Knoten einen numerischen Wert enthält der sich als gewichtete Summe der eingehenden Kanten zusammensetzt. Beispiel:

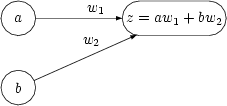
Standard Butterfly Graph

Beim Butterfly Schema fängt man so an, dass man sich erst den Vektor jeweils in ungerade und gerade Komponenten aufspaltet bis man lauter Vektoren der Länge 1 erhält. Diese schreibt man dann untereinander. Nehmen wir zum Beispiel den Vektor

a=(0123)a = \begin{pmatrix} 0\\1\\2\\3 \end{pmatrix}

Aufspalten jeweils in gerade und ungerade Teilvektoren ergibt diesen Baum

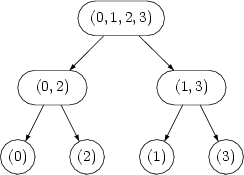
Beispielbaum

Wir schreiben nun einfach die Blätter des Baums untereinander und erhalten somit den Anfang.

Anfang des Schemas

Im ll-ten Schritt des Schemas werden nun die Rechenoperationen wie folgt dargestellt durchgeführt:

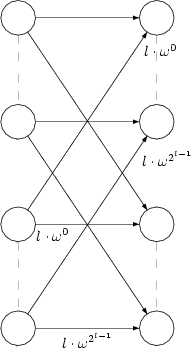
Schritt

Wir haben auf der rechten Seite den zusammengesetzten Vektor aus den beiden Vektoren halber Länge die sich auf der linken Seite befinden. Man sieht hier schön die reißverschlussartige Verschränkung. In unserem Beispiel sähe das komplette Schema folgendermaßen aus:

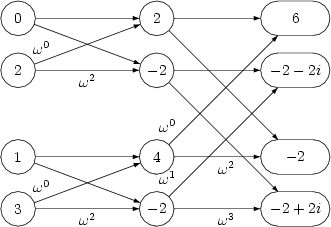
Komplettes Beispielschema

Da unser Vektor die Länge 4 hatte, haben wir folgende Werte für die Potenzen von ω\omega benutzt:

(ω0,ω1,ω2,ω3)=(1,i,−1,−i).(\omega^0, \omega^1, \omega^2, \omega^3) = (1, i, -1, -i).

Das Ergebnis ist also

b=(6−2−2i−2−2+2i).b = \begin{pmatrix}6\\-2-2i\\-2\\-2+2i\end{pmatrix}.

That’s it!

Weiteres zur FFT